Professional required course final exam in junior year of college.
#并行程序设计期末考点
-
SIMD与SPMD的区别与联系
- SIMD
多个处理单元在相同的时间周期内执行同一条指令，但处理不同的数据。典型应用是向量计算机和阵列计算机。 - SPMD
SPMD属于MIMD分类。执行的是同一个程序（运行相同的可执行文件），但是具体计算任务可以不同。
- SIMD
-
阿姆达尔定律说了什么
串行程序中如果有比例为r的部分不可并行化，那么根据阿姆达尔定律，能达到的最好加速比趋近于1/r。
比如一个程序有90%部分可以并行，那么r=1-0.9=0.1，达不到比10更好的加速比。 -
线程安全性怎么理解，怎么解决
- 线程安全性
一段代码被多个线程执行，也能获得正确的结果。 - 怎么解决
- 锁机制：确保只有一个线程在某一时刻访问共享资源
- 原子操作：保证对共享资源的操作不可分割，不会被中断
- 线程安全性
-
线程间同步的方式 互斥锁不保证同步，只保证互斥
- 信号量
- 忙等待
- 条件变量
-
CUDA的同步机制
- 核函数调用结束时同步
- 在host线程中使用
cudaDeviceSynchronize() - 保证host之后能够操作到设备计算出的结果
- 在host线程中使用
- 线程块中同步
- __syncthreads() 调用点阻塞块内所有线程，在同步点之前操作都完成
- __syncthreads_count/or/and()
- 线程束中同步
- 投票指令
- 洗牌指令
- 核函数调用结束时同步
-
原子操作的概念，并以CUDA的原子函数作为例子，说明实际的应用
- 概念：执行过程不能分解为更小的部分，不被中断
- 应用：计算直方图
1 2 3 4 5__global__ void histogram(int *histogram, int* val){ int tid = blockIdx.x * blockDim.x + threadIdx.x; int val_i = val[tid]; atomicAdd(&histogram[val_i], 1); // ++histogram[val_i] }
-
在CUDA编程中，主机内存，设备内存，统一内存寻址的概念，并说明统一内存寻址的作用
- 主机内存：CPU使用的内存
- 设备内存：GPU使用的内存
- 统一内存寻址：使主机和设备共享一个统一的地址空间。程序可以在CPU和GPU之间无缝地访问内存地址
- 作用：简化程序员视角中的内存管理，提高编程效率
-
存储体冲突的概念，结合例子说明如何解决存储体冲突
- 存储体：共享内存被分为32个同样大小的内存模型，不同存储体可同时被访问
- 串行访问：多个地址访问同一存储体
- 并行访问：多个地址访问多个存储体
- 广播访问：单一地址访问单一存储体
- 存储体冲突：多个地址访问同一个存储体（即串行）
- multicast：步长小于1的时候不存在存储体冲突
- 存储体：共享内存被分为32个同样大小的内存模型，不同存储体可同时被访问
-
OpenMP的循环依赖
-
OpenMP的静态调度
-
OpenMP的dynamic调度和Guided调度怎么选择
- dynamic 线程执行完一个chunksize之后向系统请求下一个chunk
- guided
也是执行完了才申请下一个，但是申请的chunk大小在运行中递减
在初始和结束的时候都能够做到负载均衡，比如我chunksize设置成10000，那么刚开始数据消耗得很快，然后到后面数据剩的少了，比如说只剩9999个，结果全分到一个线程去了，那么其他线程就没有事情做了。大chunksize的时候最好用guided。
-
MPI编程题
- 计算直方图
- 给一个数组
A[N]，给这个数组画一个直方图 void histogram_gen(float* A,int N, MPI_Comm comm)
-
CUDA代码效率问题分析
两个思路- 共有运算
用一个变量存运算结果，不需要反复运算。 - 内存访问不连续
- 分支分化
if..else...换成三目运算符。
- 共有运算
#自我总结
#编程例子
- 直方图计算
- 向量-向量
- 矩阵-矩阵
- 矩阵-向量
- 矩阵转置
- 全局求和
#补充概念
- SIMD和SIMT(GPU)
- GPU同样对大量元素使用相同控制流
- 但GPU不是纯粹的SIMD系统，而是SIMT
- GPU核能（相对）独立地执行指令流
- SIMT允许一条指令的多数据分开寻址，而SIMD则是连续的
- SIMT中线程具备私有寄存器，SIMD向量存在于相同地址空间
- GPU上的ALU也可能具备SIMD指令
- 线程束
线程束是GPU执行的基本单元，通常由32个并行线程组成。线程束中的所有线程是同步执行的。
- 执行方式 一个线程束内的所有线程在同一个时钟周期执行同一条指令,每个线程操作不同的数据(SIMD风格)。
- 分支分化
线程束中的线程可能会经历不同的路径(if-else)。这就会导致串行，即一个分支的所有线程执行完之后，另一个分治的才会执行。
所以一般将核函数中的if..else...改为三目运算符。三目运算符后面两个表达式都会被计算，不会分支。然后判断前面的条件，如果条件为真，丢弃后面那个结果，反之丢弃前面那个结果。三目运算符是符合CPU流水线的分支预测的，效率会比if...else...更高。 - 调度 一个线程块被分为若干线程束（例如，一个256个线程的线程块会被划分为8个线程束）。GPU调度器以线程束为单位调度和执行。
- OpenMP同步机制
#编译原理期末考点
#判断题
- DFA能否识别空串ε
- 可以，只要初始态就是接收态
- 任给一个NFA都有对应的DFA
- 正确，L(NFA)≡L(DFA)
- 左递归
- 直接左递归
A → AB - 间接左递归
A → B a | a B → A
- 直接左递归
- 在上下文无关文法中，任何一个句子都可以为其构造一棵分析树
- 每个上下文无关文法的句子都可以通过文法规则构造一棵解析树，内部节点是非终结符，叶节点是终结符
- 任给一个 LL(0)文法，它所产生的语言最多只能包含一个句子
- 错误。LL(0) 文法是一种解析简单的文法，但并不限制其语言只能包含一个句子。一个 LL(0) 文法可以生成多个句子。
- 通过合并LR(1)的状态而得到LALR(1)分析表时，合并可能会产生新的“归约—归约”冲突（Reduce-Reduce Conflict）和“移进—归约”冲突（Shift-Reduce Conflict）。
- 正确。LALR 分析表通过合并 LR(1) 状态可能会引入新的冲突。
- L-属性定义（L-Attributed Definition）适合在自顶向下的递归下降预测分析（Recursive Descent Predictive Parsing）过程中实现，不能在自底向上的 LR 分析过程中实现。
- 还不知道，忘了。
- 在语法制导翻译（Syntax-Directed Translation）技术中，回填（Backpatching）可用于解决生成跳转指令时跳转目标尚未确定的问题。
- 正确。回填技术在语法制导翻译中用于解决跳转指令目标尚未确定的问题。
- 在中间代码优化阶段，全局优化（Global Optimization）指的是跨多个子程序（如函数、过程等）进行代码调整。
- 错误。跨越基本块（Basic Block）。
- 执行中间代码优化时，需要考虑指令选择（Instruction Selection）、指令调度（Instruction Scheduling）、寄存器分配与指派（Register Allocation and Assignment）等问题。
- 错误。这是目标代码生成要考虑的事情。
#填空题
- Chomsky文法分类法
- 无限制文法
- 上下文有关文法
αAβ->αγβ - 上下文无关文法
A->γ A为非终结符，γ可以是终结符和非终结符的字符串 S->aSa | bSb | ε - 正则文法
A->a或A->aB A、B为非终结符，a是终结符，最多就两个 S -> aA A -> bB B -> cS | ε
- 句柄和活前缀
- ACTION表和GOTO表的构成
m个非终结符，n个终结符- ACTION表有
n+1个列 - GOTO表有
m个列
- 语法制导翻译SDT
- 垃圾回收算法与循环引用
- 指令序列的开销
#简答题(语义分析和中间代码生成为主)
- 给出文法，是否有二义性
- 运算符优先级，越靠近解析树根的优先级越低
- 运算符结合性，左递归左结合，右递归右结合
是有二义性的，因为它既是左递归也是右递归，结合性不清晰。E → E - E | F
- 综合属性和继承属性的判断
- 构建带注释的分析树
- 中间代码片段划分成基本块
- 画出代码的控制流图
- 优化中间代码，给出最后优化好的基本块（DAG？）
#应用题(正则、LL、LR)
-
正则
- 自然语言转正则
- 正则表达式转DFA
-
CFG LL
-
给定文法给定句子画分析树
-
文法是否适用自顶向下的分析
- 左递归消除
A -> Aα | β 消除左递归变为： A -> βA' A'-> αA' | ε 右递归 - 左公因式提取
- 左递归消除
-
求文法中的First集和Follow集
-
First集合
- RHS右手第一个是终结符直接加
- RHS右手第一个不是终结符，那就是他的First集
- 如果非终结符First里面包括ε，那么继续看下一个，直到找到终结符或者到ε
- A->CDEF，如果CDEF的First集合都有ε，那么First(A)也有ε
- 如果D的First集没有ε，那么把CD的非ε符号全部加入First(A)
-
Follow集合
- 开始符号直接先加上
$终结符 - 如有产生式A->αXβ，则把First(β)中除了ε的放入Follow(X)中 (所有Follow集不含ε)
- 如果产生式A->αX，或A->αXβ且First(β)中含有ε。那么Follow(X)+=Follow(A)，即Follow(X)包含Follow(A)
- 开始符号直接先加上
-
-
使用First和Follow构建LL(1)分析表；判断文法是否属于LL(1)
-
LL(1)表的结构
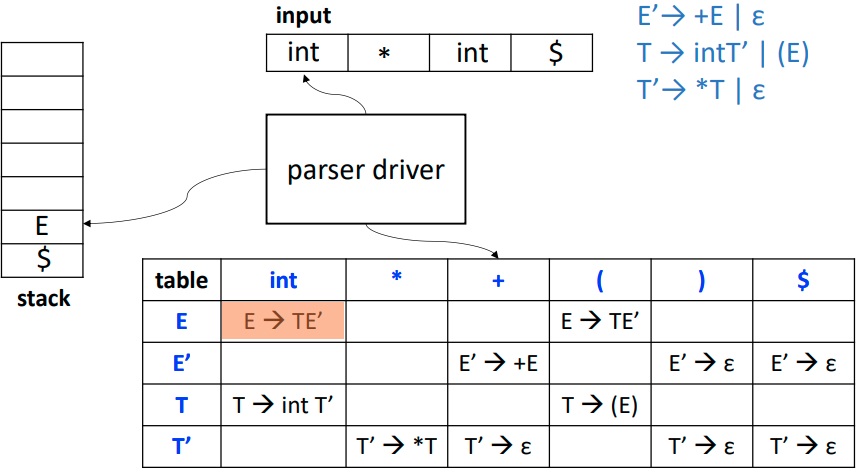※ LL(1)Table- 第一列放非终结符
- 第一行放所有终结符 + 终结符
$ - 表项放产生式
- 栈内一开始放开始符号和终止符
$ - 元素逆序入栈，这样最左的符号就在栈顶，符合最左推导
-
构建LL(1)解析表
- 将所有产生式拆分成LHS->单独RHS
- 然后看产生式RHS的First集，如果First集存在ε，那么就还要看相应LHS的Follow集
- 把RHS的First集里面包含的元素 (除了ε) 对应的列都填上对应的产生式
- 如果有ε，则把LHS的Follow里面包含的元素也填上对应的产生式
-
-
用构建的分析表列出输入串的分析过程
- 栈顶元素如果是非终结符
- Derive：用二元组（栈顶，input）访问表项，弹出栈顶，产生式逆序入栈
- 栈顶元素终结符
- Compare：比较当前的栈顶元素和input，如果不相同就是reject，如果相同弹出栈顶元素，input指针指向下一个token
- 栈顶元素如果是非终结符
-
-
CFG LR
- 求文法的增广文法，给产生式编号
- 增广文法
S'->S - 编号
记得把所有产生式的右手边的|给展开成两条产生式
- 增广文法
- LR(0)DFA
- I0就是求
S'->·S的闭包
- I0就是求
- 自动机转分析表
- LR(0)分析表的结构
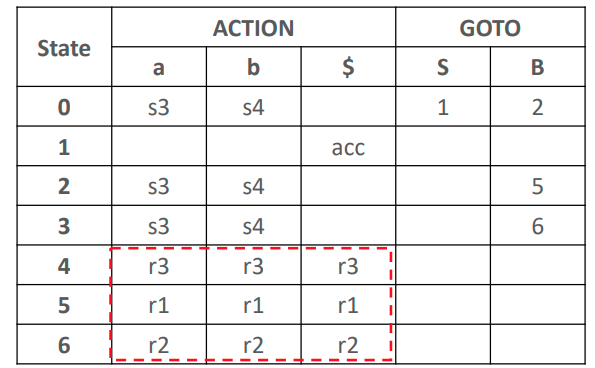※ LR(0) Table
- 第一列是state
- ACTION表第一行放所有终结符 + 终结符
$ - GOTO表第一行放所有非终结符
- 栈内一开始放状态0 + 终结符
$ - 输入buffer也要加上终结符
$
- LR(0)分析表的结构
- 用分析表分析输入串
- (栈顶，cur_input)选择动作
- Shift：移入当前input token进入栈中，且状态4也移入栈中
- Reduce：运用第4条产生式进行规约，规约出来的LHS入栈，然后根据Goto集确定state
- 某个LR(0)DFA状态是否存在冲突,SLR(1)能否解决
- SLR(1)利用的是Follow集合
- 看这个state中的shift项的下一个input token是否在待规约的N的Follow集合中
假如待规约的Follow(T)={$}，那么下一个input token(就是这里的终结符)T -> b • T -> b • E E -> • ( E ) E -> • a(a都不在Follow(T)中，所以使用SLR(1)解决了移入-规约冲突。 - LR(1)怎么改进SLR(1) 的
- 两者利⽤展望符号（Lookahead）的⽅式不同：SLR(1)简单地看Lookahead 能否跟随被归约出来的⾮终结符（即 Lookahead 必须属于该⾮终结符FOLLOW 集），⽽ LR(1)要看 Lookahead 能否跟随整个分析栈内容（即活前缀），显然⽐ SLR(1)更加精确（可跟随的符号是 SLR(1)的⼦集）。因⽽，⼀些 SLR(1)⽆法解析的冲突有可能被 LR(1)解析。
- 给出LR(1)DFA初始状态
- 初始状态怎么给现在还是不太清楚
- 这次考试考LR(1)DFA的可能性很大
- 求文法的增广文法，给产生式编号